MRRからACVを概算する

CEO「MRRからACVって計算できないんだっけ？」

わし「ふむ、それは頑張れば出来ると思うが、まあまあ頑張らないといけない。ちょっとやってみる」

予算や事業計画を立てる際、いくつかの指標をもとにしてMRRを算出するところまでは難しくありません。 しかし事業特性によっては、ACV（契約金額ベース）の推移を見ないと、サブスクリプション事業で資金繰りがうまくいくのかが判断しにくいケースがあります。 そこでMRRからACVを算出する方法について数学的に正しいそうな方法を考えてみました。

MRRとかACVってなにもの？

両方ともサブスクリプションモデルにおける収益指標ですが、収益を認識するタイミングが以下の様に違います。

• MRR(Monthly Recurring Revenue): サービスが提供された時点
• ACV(Annual Contract Value): 契約発生時点(ただし契約期間を1年を限度にしてみなしたもの)

以下のグラフで例を見てみると分かりやすいです。

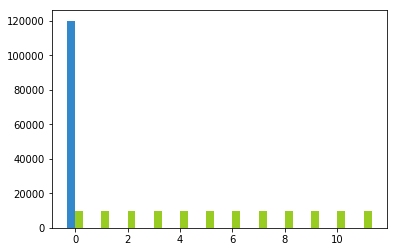
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

# 月10000の年間契約
acv = np.array([120000])
acv_months = np.array(range(len(acv)))
mrr = np.array([10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000])
mrr_months = np.array(range(len(mrr)))

ax = plt.subplot()
ax.bar(acv_months-0.15, acv, width=0.3, color="#3388cc")
ax.bar(mrr_months+0.15, mrr, width=0.3, color="#99cc22")
plt.show()

青がACVで緑がMRR

ACVの系列からMRRの系列を概算するには

まず、「全ての契約が年間契約」という適当な仮定をおきます。 この前提のもとで定式化することで説明が簡単になります。違和感がある場合、自社の平均契約月数を使用したり、MRRを契約期間で色分けなどをすることでより正確な計算ができるはずです。

まず、 をACVの列、 をMRRの列とすると、以下のような関係式があると言えます。

この式は、12ヶ月以内にACVとして発生した分をそれぞれ足して12で割った分ですので、ACVの定義から直感的に理解できます。

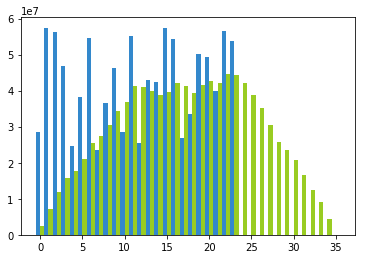
ACVに対し、MRRがどのように発生してくるかを、実際に適当にランダムなACV系列からMRR系列を出してみると以下のようになります。

# 24ヶ月分のACV系列 (20,000,000 ~ 60,000,000)
acv = np.random.randint(20000000, 60000000, 24)
acv_months = np.array(range(len(acv)))

# 便宜のために配列の範囲外は0とみなす関数を用意
def get_acv(m):
    return acv[m] if 0 <= m and m < len(acv) else 0

# MRRは少なくともACVより12ヶ月長い
mrr_months = np.array(range(len(acv) + 12))

# m月のMRRを計算
def calc_mrr(m):
    backs = range(12)
    acvs = map((lambda x: get_acv(m - x)), backs)
    return sum(acvs)/12.0

mrr=list(map(calc_mrr, mrr_months))

ax = plt.subplot()
ax.bar(acv_months-0.25, acv, width=0.5, color="#3388cc")
ax.bar(mrr_months+0.25, mrr, width=0.5, color="#99cc22")
plt.show()

逆にMRRの系列からACVの系列を概算するには

ACV→MRRはシンプルに計算できましたが、MRR→ACVには少しテクニックを要します。 上の関係式をもりもり変形していくと..

となります。

最後の式の右辺は無限和になっていますが、実際にはMRRを過去に遡るとどこかで0になるので、有限和として計算することができます。

これが実際にACVになることを、前半で生成したMRRから元のACV列を構成できるかどうかを見て検証してみます。

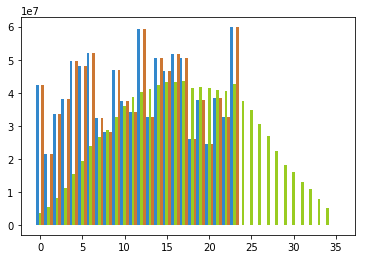
# 先程のMRR配列を、ACVの時と同じように範囲外を0とみなすようにする
def get_mrr(m):
    return mrr[m] if 0 <= m and m < len(mrr) else 0

# MRRを使用してACVを概算する
def calc_acv(m):
    year_backs = range(int(m / 12) + 1) # 計算が有限になるように
    mrr_diffs = map((lambda x: get_mrr(m - 12 * x) - get_mrr(m - 12 * x - 1)), year_backs)
    return 12.0 * sum(mrr_diffs)

reversed_acv = list(map(get_acv, mrr_months))

ax = plt.subplot()
ax.bar(acv_months - 1.0/3.0, acv, width=1.0/3.0, color="#3388cc")
ax.bar(mrr_months, mrr, width=1.0/3.0, color="#99cc22")
ax.bar(mrr_months + 1.0/3.0, reversed_acv, width=1.0/3.0, color="#cc7733")
plt.show()

茶色が再計算されたACV。MRRの元となっているACVと一致していることがわかります。

ACV→MRRで均されて情報量が減ったかと思いきや、逆変換できるって面白いですね😮

www.wantedly.com